 | VベルトのV角が40°と決められた理由を教えて下さい. |
 | Vベルトはくさび効果を用いてプーリを押す力を高めることができ,V溝の角\(\alpha\)を小さくすればその効果は大きくなり、その計算式から伝達力が増すことは周知と存じます.実際のVベルト伝動には,伝達能力が大きくなると共に、プーリヘのベルトの出入りがスムーズに行われることが必要となります.そのため,プーリのV溝の角度\(\alpha\)とV溝の半径方向の摩擦係数\(\mu_r\)との間に次の条件が必要となります. V溝の角度\(\alpha\)が0<\(\alpha\)≦\(\pi\)の範囲において,ベルトがプーリV溝斜面を押す力NとベルトをV溝に押し込む力Fとの関係はN ≧\(\frac{F}{2}\)であるためVベルトがプーリから離れるとき,プーリ溝から離れる力F´とNの関係は, \(N=\frac{F’}{2(sin(\frac{\alpha}{2})-\mu_r cos(\frac{\alpha}{2}))}\) で,巻き付いて安定したときと異なりこの式で\(sin(\frac{\alpha}{2})-\mu_r cos(\frac{\alpha}{2})\) ≦ 1になります.この式を移行すると\(1 – sin(\frac{\alpha}{2})\)≧\(\mu_r cos(\frac{\alpha}{2})\)と表わせます. また,張力でベルトを溝に押し込む力Fとベルトを引き抜く力F´の関係がF´<Fになればベルトがプーリ溝より抜けなくなります.そのためこの2つの力はF´≧Fである必要があります.言い換えると, F´≧F = \(2 N sin(\frac{\alpha}{2})-\mu_r cos(\frac{\alpha}{2})\)≧0 の関係が成立する必要があります.ここで,\(sin(\frac{\alpha}{2})-\mu_r cos(\frac{\alpha}{2})\) ≧ 0 となります. これを移行し\(sin(\frac{\alpha}{2})\) ≧ \(\mu_r cos(\frac{\alpha}{2})\) で表され,摩擦係数は\(\mu_r\) ≦ \(tan(\frac{\alpha}{2})\),また,\(\frac{\alpha}{2}\) ≧ \(tan^{-1}(\mu_r)\)とも表わせます.ここで,\(tan^{-1}(\mu_r)\)は摩擦角とも言われ,V溝の角\(\alpha\)の半分値は摩擦角よりも大きくなくてはいけないことをこの式は示しています。言い換えると,F´= F = \(2 N sin(\frac{\alpha}{2})-\mu_r cos(\frac{\alpha}{2})\) ≧ 0の関係が成立しない場合,ベルトを押し込む力F がなくなっても,ベルトはプーリ溝中から抜け出ないことになります。 図に,このVベルトの角度\(\alpha\)と摩擦係数\(\mu\)との関係でV溝の限界角を示します。くさび効果を有効に発揮して円滑に伝達するためには,図に示される線図「\(1-sin(\frac{\alpha}{2})\)」,「\(\mu_r cos(\frac{\alpha}{2})\)」,「\(sin(\frac{\alpha}{2})\)」に囲まれた領域で\(\alpha\)の1/2を設定します。図中の太い赤線は\(\mu_r\) = 0.3の領域を示し,このときのVベルトの角度は18゜≦ (\(\frac{\alpha}{2}\)) ≦ 57°の角度範囲となります。このことから,V溝の角を40度とすることは妥当な値とされます. これらの解説はベルト伝動技術懇話会の書籍「ベルト伝動・精密搬送の実用設計」(養賢堂)に掲載しております. また,この角度は,相当以前から決められており、多様な使用条件(環境、負荷)で使用され、ベルトの強度(寿命)から妥当な値とされたものと思われます. 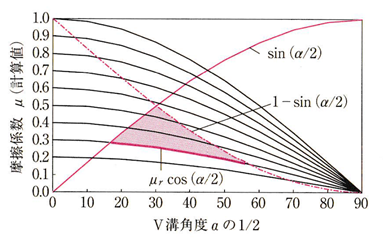 V溝の角度限界 |
V角の根拠を教えてください

 4 人が参考になったと評価しました
4 人が参考になったと評価しました


