ベルトを用いた伝動系を理解する場合に有効な理論として，Eularの摩擦伝動理論は古典的ではありますが，非常に有用です．

ベルトに張力\(T_t=T_s=T_p\)を与えて原動プーリ（プーリ1）と従動プーリ（プーリ2）に巻きつける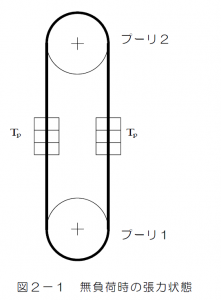．この状態でベルトを回転させても，軸受などでエネルギ損失がなければ，理論的には二つのプーリ間で動力は伝達されない．

図2-1は無負荷伝動の状態を静止状態に模擬して示したものである．今，原動プーリに負荷を与えると，二つのプーリをつなぐベルト間に張力差が生じる．

図2-2は，動力が伝えられている状態を模擬して示す．従動プーリに負荷が加わると\(T_t\)と\(T_s\)のバランスが崩れて\(T_t > T_s\)となり，この張力差により原動プーリから従動プーリに動力が伝えられる．ここで，\(T_t\)を張り側張力，\(T_s\)をゆるみ側張力と呼ぶ．また，ベルトが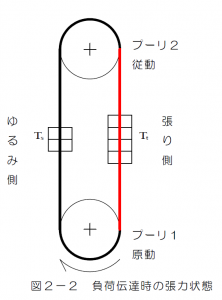取り付けられた状態での張力\(T_p\)を初張力または静止張力といい，\(T_t\)と\(T_s\)の張力差は有効張力\(T_e\)と呼ばれ，下式で表される．

\(T_e=T_t-T_s\)　　　(2-1)

今，プーリ上でのベルト張力の変化について考える．摩擦伝動ベルトの最も基本的な式としてEulerの式（Einterweinの式とも呼ばれる）がある．この式は使用されるパラメータを少なく簡単であるため，平ベルト，Vベルト，Vリブドベルトを問わず，現在でも摩擦伝動ベルトの設計計算を行う上で広く用いられている．このEulerの式は，ベルトとプーリ間の力の伝達を次のような仮定に基づいて導く．

• ベルト，プーリ間の摩擦係数は一定である．
• ベルトはプーリ径に対して十分薄いものとする．すなわち，ベルトの曲げ変形による作用は考えない．

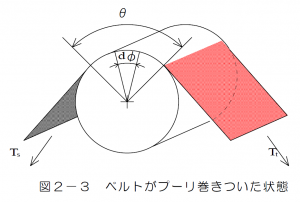
図2-3は，角速度\(\omega\)で回転するプーリに巻きついたベルトを示す．ここで，接触角度（ベルトとプーリが接触している円弧に対する中心角）を\(\theta\)とする．図中，図示する位置，ゆるみ側入り口を角度\(\phi\)の原点とし，\(\phi\)離れた位置での微小要素（角度\(d\phi\)を考える．後述で述べるように，ベルトのプーリ入り口では，ベルトがプーリと連れ回る休止角（idle arc）がある．したがって，\(\phi\)の原点は入口側ベルト張力が変化し始める位置とするのが正確である．

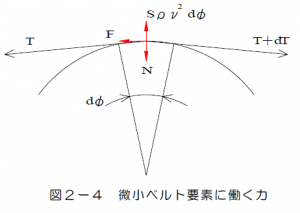
図2-4は，その微小ベルト要素に作用する力を図示したものである．微小ベルト要素にはベルト張力\(T\)，\(T+dt\)，摩擦力\(F\)，プーリからの反力\(N\)，および遠心力（\(S \rho R^2 \omega ^2 d \phi = S \rho v^2 d \phi = m v^2 d \phi\)）が作用する．したがって，プーリ半径方向の力のつり合いより，反力\(N\)は

\(N=Tsin(\frac{d\phi}{2})+(T+dT)sin(\frac{d\phi}{2})-mv^2d\phi\)

\(=2Tsin(\frac{d\phi}{2})+dTsin(\frac{d\phi}{2})-mv^2d\phi\)　　　(2-2)

ここで，\(S\)，\(\rho\)，\(m\)，\(R\)および\(v\)は，それぞれベルトの断面積，密度，単位長さ当りの質量，ベルトピッチ円半径およびベルト速度（周速）である．\(d\phi\)が微小であることから，\(sin(\frac{d\phi}{2}) = \frac{d\phi}{2}\)とおける．また，\(dT\)も微小であることから，上式は次のようになる．

\(N=(T-mv^2)d\phi\)　　　(2-3)

ベルト・プーリ間の最大摩擦係数を\(\mu\)とすれば，摩擦力\(F\)は次式で与えられる．

\(F=\mu N\)　　　(2-4)

図2-4でプーリ円周方向の力のつり合いを考えると，

\(\{(T+dT)-T\}cos(\frac{d\phi}{2})-F=0\)　　　(2-5)

が得られる．式(2-3)および式(2-4)を式(2-5)に代入すると，

\(dTcos(\frac{d\phi}{2})=\mu(T-mv^2)d\phi\)　　　(2-6)

となる．\(d\phi\)が微小であることから，\(cos(\frac{d\phi}{2})=1\)とおける．したがって，上式は次のようになる．

\(dT=\mu(T-mv^2)d\phi\)　　　(2-7)

即ち，

\(\mu d \phi=\frac{dT}{T-mv^2}\)　　　(2-8)

これを積分して，

\(\phi=(\frac{1}{\mu})\ln{(T-mv^2)}+C\)　　　(2-9)

ここで，\(C\)は積分定数である．境界条件\(\phi=0\)のとき\(T=T_s\)より，

\(T=T_s e^{\mu \phi}+(1-e^{\mu \phi}) m v^2\)　　　(2-10)

また，\(\phi=\theta _0\)のとき\(T=T_t\)より，

\(e^{\mu \phi}=\frac{T_t-mv^2}{T_s-mv^2}\)　　　(2-11)

\(\theta_0\)はベルトとプーリの接触角のうち，ベルトとプーリ間で動力の授受が行われている領域を示し，クリープ角（active arc）と呼ばれる．\(\theta_0 < \theta\)（ベルトの接触角度）であり，\((\theta-\theta_0)\)では動力の伝達が行われず，休止角と呼ばれる． 今，有効張力を\(T_e\)とすると，式(2-1)および式(2-11)から，次式が与えられる． 張り側張力 \(T_t=T_e \frac{e^{\mu \theta _0}}{e^{\mu \theta _0}-1}+mv^2=T_e \frac{e^{\mu \theta _0}}{e^{\mu \theta _0}-1}+T_c\)　　　(2-12) ゆるみ側張力 \(T_s=T_e \frac{1}{e^{\mu \theta _0}-1}+mv^2=T_e \frac{1}{e^{\mu \theta _0}-1}+T_c\)　　　(2-13) 上式で，\(T_c\)（\(=mv^2\)）は遠心張力と呼ばれ，プーリ上で放射線状に働く遠心力の水平分力がベルトの張力として働く．