推力を与えない固定プーリにVベルトを巻きつけて回転させています．推力を与えることが出来ないため，軸間力制御をしています．そこで，軸間力から推力を求めるためにはどうのようにすればいいですか(式など)？ご回答よろしくお願いします．

Vベルトがプーリに押しつけられることによって生じる軸方向の力(推力)の式は，ベルト式CVTにおいて加減速するためにシーブを軸方向に移動させるプーリ推力の場合と同様に考えることにより求めることができます(1)(2)． プーリ溝に作用するVベルトの推力Qは，Vベルトが圧縮やせん断変形を生じないと仮定して，プーリに巻付いたVベルトをn個のブロックに分割して考えます(1)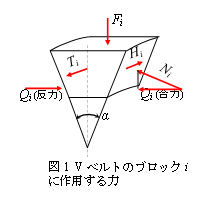．図1に，n個のブロックの内，i個目に作用しているそれぞれの力を示します．今，ブロックiがプーリ溝にFiの力で押し付けられ，ブロックの両側面にそれぞれ法線方向の反力Niが作用したとします．この状態からブロックiが張力Tiで引っ張られたとき，ブロック両側面の円周方向に摩擦力Hiが生じ，これがプーリの回転力になります．このとき，Hiは次式で表されます． \(H_i = \mu N_i\) (1) ここで，\(\mu\)は\(T_i\)が作用したことによるブロックとプーリ間に生じる動力伝達に必要な円周方向の摩擦係数です， 式(1)の摩擦力\(H_i\)はブロックiの両側面で作用しており，これらのi = 1からnまでの総和が有効張力Teになりますので，\(T_e\)は次式で表されます． \(T_e = 2 \sum_{i=1}^n H_i = 2 \mu \sum_{i=1}^n N_i\) (2) ここで，式（２）の両辺に\(cos (\alpha / 2)\)を乗じますと \(T_e cos(\frac{\alpha}{2}) = 2 \mu \sum_{i=1}^n N_i cos(\frac{\alpha}{2})\) (3) が得られます．このとき，式（３）中の\(N_i cos(\frac{\alpha}{2})\)がブロックiに作用する推力\(Q_i\)になりますので，推力の総和Qは \(Q = \sum_{i=1}^n N_i cos(\frac{\alpha}{2})\) (4) で与えられます．従って，式(4)を式(3)に代入すると，Qは次式により得られます． \(Q = \frac{T_e cos(\frac{\alpha}{2})}{2 \mu}\) (5) 初張力を\(T_0\)，張り側張力を\(T_t\)，ゆるみ側張力を\(T_s\)とし，ベルトの曲げ剛性と遠心張力を無視したとき，\(T_0 \simeq (T_t + T_s) /2\)であると仮定します．また，プーリに巻付いたベルトの張力変化がEulerの理論に従うものとしますと，有効張力\(T_e\)は次式で表されます． \(T_e = 2 T_0 (\mathrm{e}^{\mu ‘ \theta}-1)(\mathrm{e}^{\mu ‘ \theta}+1)\) (6) ここで，ここで，\(\mu ‘\)は「見かけの摩擦係数」で，\(\mu ‘ = \mu / \{ sin(\alpha / 2) + \mu cos(\alpha/2) \}\)です．また，\(\theta\)はVベルトとプーリ間で動力伝達の授受が行われる巻付け角です． \(T_0\)の2倍が軸荷重(軸間力)Wですので，QとWの関係は，式(6)を式(5)に代入して，次式により得られます． \(Q = W (\mathrm{e}^{\mu ‘ \theta}-1)cos(\frac{\alpha}{2}) / 2\mu(\mathrm{e}^{\mu ‘ \theta}+1)\) (7) 式(7)は，Vベルトとプーリ間の半径方向の力がつりあっているとき，Wにおける最大伝達力時のQを示しています．結果的に，CVTベルトのようにシーブを可動させる場合も(1)(2)，VベルトのようにV溝が固定されている場合もQの値は同様になります． その他，Vベルトの半径方向の移動に関する条件などにつきましては，文献(1)(2)をご参照ください．

参考文献

1. ベルト伝動技術懇話会編，新版 ベルト伝動・精密搬送の実用設計，2006年8月養賢堂発行，pp. 103-107．
2. 網島貞夫著，工業用伝動ベルト，1968年9月オーム社発行，PP. 187-194．