タイミングベルトが蛇行する時の力を求めたいのですが、プーリに巻きつく角度を180度すると、 [math]N=(T-mv^2)d\phi[/math] より[math]mv^2[/math]が無視できれば [math]N=T\pi[/math] プーリとベルトの摩擦係数を[math]\mu[/math]とすると蛇行するときの力は [math]F=T\pi\mu[/math] ということになりませんか？

ベルトの蛇行は，周期性の幅方向の移動であり，ベルト自体の製作（張力バランスの違い）や幅裁ち加工等の不備で発生するもので，本来，力を計算で求められないものと考えています．一方，軸の平行度，プーリの面振れなどにより，ベルトの軸方向への移動（片寄り）が考えられます． ご質問の[math]F[/math]は，蛇行に関するファクタが含まれていませんので，この場合，蛇行するときの力ではなく，ベルトが軸方向に移動しようとするときの抑止力と考えられます． 歯付ベルトの蛇行を片寄りの範疇で考えますと，ベルトの軸方向に作用するかみあい始めの1歯目の力[math]F_1[/math]（片寄り力）は，下図に示しますように，1歯目のベルトの進入角を[math]\phi_1[/math]，ベルト歯面荷重を[math]Q_1[/math]とすると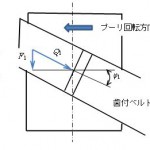， [math]F_1=Q_1sin\phi_1[/math] で与えられ，かみ合い歯数をnとすると，総軸方向荷重[math]F[/math]は次式で表されます． [math]F=\sum_{k=1}^{n}Q_ksin\phi_k[/math] なお，任意の歯数k歯目のQkを求めるための荷重分担計算に関する概略は文献(1)を，詳細につきましては，文献(2)，(3)をご参照ください．また，片寄りにつきましては，はすば歯付ベルトですが，文献(4)をご参照いただき，ねじれ角を進入角と置き換えて見ていただければ片寄りの発生機構がご理解いただけるものと思います．

参考文献
(1) ベルト伝動技術懇話会編，ベルト伝動・精密搬送の実用設計，養賢堂，pp. 122-124．
(2) 小山他，歯付ベルトの強度に関する研究(第4報，不完全かみあい部を考慮した荷重分担)，日本機械学会論文（C編），45巻399号(1979-11)，pp. 1269-1276．
(3) 籠谷他，歯付ベルトの初張力作用時における荷重分担，日本機械学会論文（C編），49巻448号(1983-12)，pp. 2212-2219．
(4) 籠谷他，正逆回転時におけるはすば歯付ベルトの回転伝達誤差(伝達トルク作用時の場合)，日本機械学会論文（C編），72巻713号(2006-1)，pp. 219-227．